Blog Irma Robles : noviembre 2017

jueves, 30 de noviembre de 2017

Módulo 14 Semana1 Prepa en Línea SEP "El átomo"

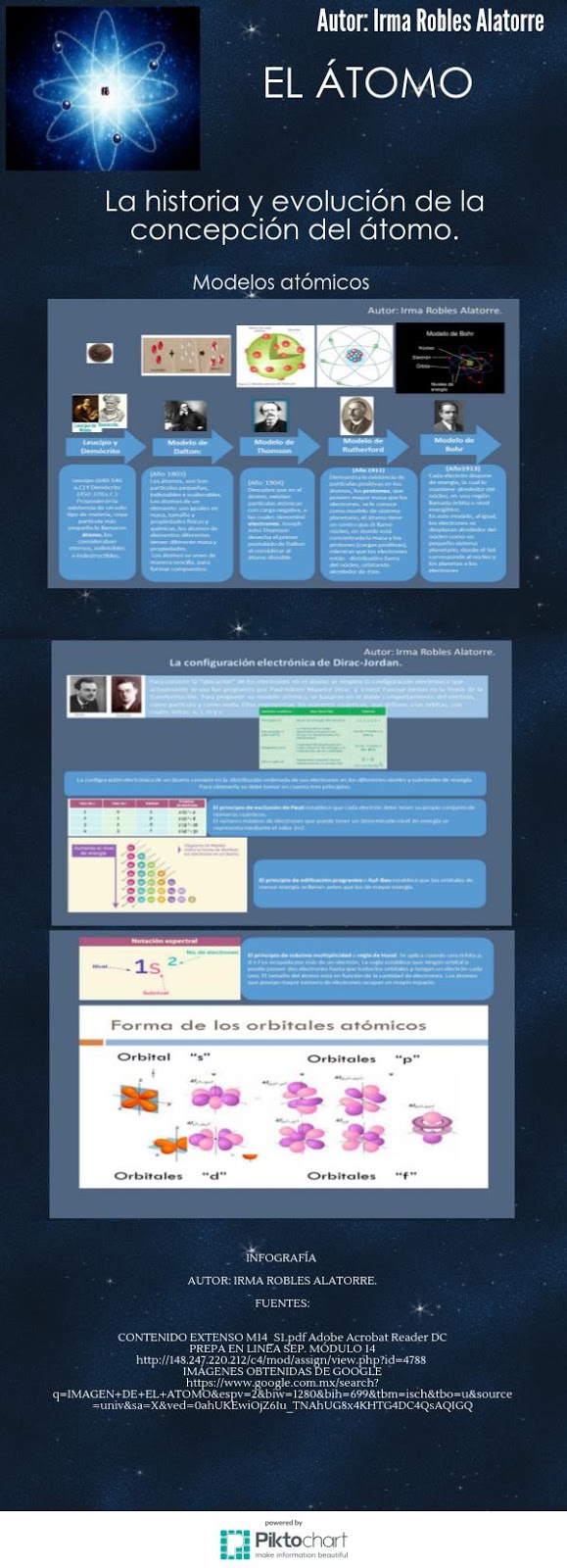
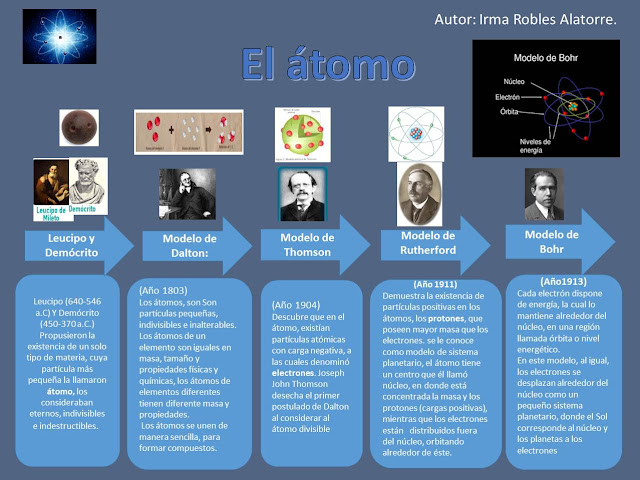
Para que se aprecie mejor cada parte de la infografía:

miércoles, 22 de noviembre de 2017

Módulo 14 Semana 4 "El plato del bien comer." Prepa en Línea SEP

El objetivo de este proyecto es elaborar un documento donde se analice, a partir de un caso, la importancia de la nutrición completa y variada, como lo establece el “plato del bien comer”, para el buen funcionamiento de los procesos vitales del ser humano.

La alimentación de Carlos y Carmen

Carlos es un contador de 40 años, debido a su trabajo sus horarios laborales son muy variados y extremos, el horario oficial es de 9 a 6; sin embargo hay ocasiones en que permanece en la oficina hasta después de las 10 de la noche. Además de esto, aun cuando tiene establecida una hora de comida, en ocasiones tiene que comer en menos tiempo, para evitar retrasarse.

Carmen es abogada y tiene 45 años de edad. Tiene un hijo de 9 años. Trabaja en una oficina de 8 a 5, y tiene una hora para comer. Generalmente llega a casa a las 6 de la tarde y debe realizar diversas actividades, como: limpiar la casa, comprar la despensa, preparar comida para su familia y ayudar a sus respectivos hijos con algunas tareas escolares.

Tanto Carlos como Carmen han seguido una dieta muy poco variada durante los últimos 10 años, generalmente en un día común sus alimentos son:

2. Incluir las respuestas a las siguientes preguntas, a partir del análisis del caso.

a. ¿Qué tipo de biomoléculas (carbohidratos, lípidos y proteínas) se observan prioritariamente en las dietas de Carlos y Carmen?

En la dieta de Carlos podemos observar que es rica en carbohidratos, lípidos y proteínas de la carne que consume sin embargo al ser comida que se compra en la calle no es muy sana y abusa del refresco y bebidas energéticas, casi no consume agua.

La dieta de Carmen es rica en carbohidratos pero no consume casi nada de proteínas ni de lípidos, ella si toma agua suficiente para su organismo.

b. ¿Qué tipo de alimentos hacen falta en cada una de las dietas para cumplir con el “plato del bien comer”?

Es muy importante consumir todos los grupos de alimentos a los dos les hace falta consumir frutas, verduras, leguminosas, pollo, pescado, en el caso de Carlos consumir frutas y verduras preferentemente con cascara, cereales integrales, leguminosas, las carnes blancas, como pollo y pescado, aumentar su consumo de agua. Carmen debe agregar, proteínas de origen animal, leguminosas, frutas y verduras.

c. Si la dieta de ambos continuara así, menciona una repercusión que podría tener el organismo de cada uno por la falta de algunos alimentos.

En Carlos su organismo se vería afectado por la mala alimentación, por el exceso de carbohidratos lípidos y proteínas a largo plazo podría presentar problemas de obesidad, triglicéridos, colesterol y diabetes, y por la falta de consumo de agua problemas renales. Además el sobrepeso y la obesidad afectan la salud, figura, bienestar y estado de ánimo: son el principal factor de riesgo para desarrollar enfermedades crónicas como: presión alta, diabetes, infartos, embolias, algunos tipos de cáncer, problemas de huesos y articulaciones, depresión, baja autoestima.

En Carmen aunque aparentemente trata de comer sano, no cubre los nutrientes necesarios para que su organismo funcione correctamente. Ningún alimento contiene todas las sustancias nutritivas que tu cuerpo necesita, por lo que se debe incluir diariamente alimentos de los tres grupos y variarlos, esta dieta tan poco variada, podría provocarle problemas de huesos y articulaciones, trastornos menstruales, depresión, baja autoestima, una deficiencia de hierro, anemia o una baja de defensas por la falta de vitaminas, lípidos y proteínas.

Además el consumir alimentos en la calle corren el riesgo de que puedan estar poco higiénicos y esto puede provocar problemas infecciosos y parasitarios.

d. Construye una dieta para cada uno, que incluya el “plato del bien comer”, basado en la NOM-043-SSA2-2005, que puedan llevar con su estilo de vida.

Horario	Carlos (opciones)	Carmen (opciones)
Desayuno	· Licuado de frutas con leche de almendras y cereal. · Sándwich integral con panela, cebolla, jitomate, espinacas y zanahoria rayada. · Tres quesadillas de maíz con panela y champiñones, acompañadas de ensalada verde. · Sopa de lentejas y dos quesadillas.	· Licuado de frutas con leche de almendras y cereal. · Sándwich integral con panela, cebolla, jitomate, espinacas y zanahoria rayada. · Dos quesadillas de maíz con panela y champiñones, acompañadas de ensalada verde.
Colación	· Dos frutas de su elección · Pan y cafe · 2 tasas de melón	· Dos piezas de fruta · Dos tazas de melón · Café y galletas.
Comida	· 200gr pechuga de pollo, ensalada verde,1 taza de espagueti y tortilla de maíz · Picadillo de soya, frijoles cocidos, 1 taza de verduras, tortilla de maíz y salsa mexicana. · 180gr de pescado a la plancha, 1/2 taza de arroz integral y sopa de verduras, galletas habaneras. · Ensalada de atún con verduras, pasta de sopa y galletas habaneras. · Bistec asado, frijoles tortilla de maíz y verduras cocidas · Coctel de camarones, cebolla, jitomate, cilantro y aguacate con tostadas	· 100gr pechuga de pollo, ensalada verde, espagueti y tortilla de maíz · Picadillo de soya, frijoles cocidos, 1 taza de verduras, tortilla de maíz y salsa mexicana. · 120gr de pescado a la plancha, 1/2 taza de arroz integral y sopa de verduras, galletas habaneras. · Ensalada de atún con verduras, pasta de sopa y galletas habaneras. · Bistec asado, frijoles tortilla de maíz y verduras cocidas
Colación	· Jícama, pepino y mango · Gelatina y fruta.	· Jícama, mango · Gelatina y Manzana
Cena	· Yogurt natural con fruta y 10 mitades de nuez. · Licuado de leche, plátano, salvado y almendras · Fruta con queso cottage y dos cucharadas de nuez picada. · Cereal con leche y fruta.	· Yogurt natural con fruta y 10 mitades de nuez. · Licuado de leche, plátano, salvado y almendras · Fruta con queso cottage y dos cucharadas de nuez picada. · Cereal con leche y fruta.

e. ¿Por qué es importante para Carlos y Carmen tener una buena nutrición?

La alimentación correcta es la base de una buena salud junto con el consumo de agua simple potable y la práctica diaria de actividad física, es la mejor manera de prevenir y controlar el sobrepeso, obesidad y otras enfermedades, como la diabetes y presión alta, entre otras. Por lo que es muy importante, asegurar tener una alimentación correcta a lo largo de toda la vida. La alimentación correcta está representada gráficamente en el Plato del Bien Comer, que muestra los tres grupos de alimentos que deben estar presentes en las tres comidas principales del día:

Verduras y frutas: Principal fuente de vitaminas, minerales, antioxidantes y fibra dietética

Cereales y tubérculos: Principal fuente de hidratos de carbono

Leguminosas y alimentos de origen animal: Principal fuente de proteínas

Esta alimentación deberá ser acompañada del consumo de agua recomendado como mínimo 2litros al día, para tener lo que nuestro organismo necesita.

f. ¿Qué repercusiones favorables tendrá el que ellos mejoren su alimentación basada en el plato del bien comer?

Si practican el hábito de una alimentación saludable, tendrán grandes beneficios, su sistema inmunológico se fortalece, mejora el aspecto de su piel y cabello, tendrán mayor energía para cumplir con sus actividades, su salud general mejorará notablemente, al consumir los alimentos de los tres grupos del plato del bien comer, esto además servirá de ejemplo y beneficiará la salud de su hijo al alimentarlo con las biomoléculas (carbohidratos, lípidos y proteínas) tan necesarias para un sano desarrollo, si dejan de consumir alimentos en la calle y dejan el refresco su economía se verá beneficiada y con esto podrán comprar alimentos nutritivos, en fin el cambio de hábitos transformara favorablemente la calidad de vida de la familia.

FUENTES:

Prepa en Línea SEP. (2016) Módulo 14.http://148.247.220.212/c4/mod/assign/view.php?id=4874

Los contenidos de la Unidad 3, temas: bioelementos; biomoléculas, estructura y funciones; y nutrición. Contenido extenso del módulo 14. M14_S4.pdf Adobe Acrobat Reader DC

http://www.diabetesbienestarysalud.com/2013/07/un-plato-muy-mexicano-el-plato-del-buen-comer/

http://www.imss.gob.mx/sites/all/statics/salud/guias_salud/adolescentes/guiaadolesc_nutricion.pdf

jueves, 16 de noviembre de 2017

Módulo 14S3 Prepa en Línea SEP Actividad: "Leyes de Newton"

LEYES DE NEWTON

INTRODUCCIÓN:

Las leyes de Newton, también conocidas como leyes del movimiento de Newton, son tres principios a partir de los cuales se explican la mayor parte de los problemas planteados por la mecánica, en particular aquellos relativos al movimiento de los cuerpos, que revolucionaron los conceptos básicos de la física y el movimiento de los cuerpos en el universo.

Las leyes enunciadas por Newton, son consideradas como las más importantes de la mecánica clásica, son tres: la ley de inercia, la relación entre fuerza y aceleración y la ley de acción y reacción. Newton planteó que todos los movimientos se atienen a estas tres leyes principales, formuladas en términos matemáticos. Un concepto es la fuerza, causa del movimiento y otro es la masa, la medición de la cantidad de materia puesta en movimiento; los dos son denominados habitualmente por las letras F y m.

La primera ley de Newton dice: “Todo objeto continúa en su estado de reposo o de movimiento uniforme en línea recta, a menos que sea obligado a cambiar ese estado por fuerzas que actúan sobre él”. En esta expresión tanto la fuerza como la aceleración llevan dirección y sentido.

La segunda ley de Newton complementa a la primera: “La fuerza neta que actúa sobre un objeto, es proporcional a la aceleración que adquiera al moverse, y a la masa de dicho objeto” Es decir, la Fuerza es igual a masa por aceleración, traducido a fórmula sería: F = m x a.

La tercera ley de Newton establece lo siguiente: Siempre que un objeto ejerce una fuerza sobre un segundo objeto, este ejerce una fuerza de igual magnitud y dirección pero en sentido opuesto sobre el primero. Con frecuencia se enuncia así: A cada acción siempre se opone una reacción igual pero de sentido contrario.

En la presente actividad realizaré un reporte de práctica de un experimento que compruebe la tercera ley de Newton y lo representaré con imágenes que demuestren lo que se hizo, como se hizo y lo que obtuve de resultados finales, el experimento demostrará de manera sencilla como golpear un balón con el pie se ejerce una fuerza sobre él y el balón a su vez ejerce una fuerza de resistencia a moverse que se ejerce con la misma intensidad pero en dirección contraria hacia el objeto(pie) que lo golpea cumpliendo así, con la tercera ley de Newton.

TEORIA:

Tercera ley de Newton o principio de acción y reacción.

La tercera ley de Newton establece lo siguiente: siempre que un objeto ejerce una fuerza sobre un segundo objeto, este ejerce una fuerza de igual magnitud y dirección pero en sentido opuesto sobre el primero.

Con frecuencia se enuncia así:

A cada acción siempre se opone una reacción igual pero de sentido contrario. En cualquier interacción hay un par de fuerzas de acción y reacción situadas en la misma dirección con igual magnitud y sentidos opuestos.

La palabra fuerza es crucial en esta ley, se necesita la interacción entre dos fuerzas para cumplir la ley.

Podemos observar esta ley todo el tiempo, basta con que existan dos objetos en contacto, también se puede enunciar de la siguiente manera “No puedes tocar sin ser tocado”. (Contenido extenso)

Aplicaciones de la Tercera Ley de Newton

Algunos ejemplos donde actúan las fuerzas acción-reacción son los siguientes:

Un pez empuja el agua hacia atrás con las aletas, por lo que el agua empuja al pez hacia adelante.

Como ya vimos al patear una pelota, el pie ejerce una fuerza sobre ésta; pero, al mismo tiempo, puede sentirse una fuerza en dirección contraria ejercida por la pelota sobre el pie.

Si una persona empuja a otra de peso similar, las dos se mueven con la misma velocidad pero en sentido contrario.

Cuando saltamos, empujamos a la tierra hacia abajo, que no se mueve debido a su gran masa, y esta nos empuja con la misma intensidad hacia arriba.

Una persona que rema en un bote empuja el agua con el remo en un sentido y el agua responde empujando el bote en sentido opuesto.

Cuando caminamos empujamos a la tierra hacia atrás con nuestros pies, a lo que la tierra responde empujándonos a nosotros hacia delante, haciendo que avancemos.

Cuando se dispara una bala, la explosión de la pólvora ejerce una fuerza sobre la pistola (que es el retroceso que sufren las armas de fuego al ser disparadas), la cual reacciona ejerciendo una fuerza de igual intensidad pero en sentido contrario sobre la bala.

RESULTADOS:

Tenemos: El pie (objeto A) golpea el balón con fuerza de 4k. Balón (objeto B) masa .450k

Aquí convertimos los kilos de fuerza a newton, tenemos que: 1k = 9.80665002864newton

9.80665002864 x 4 = 39.22660011456newton

Ahora sabemos que la fuerza del golpe al balón es de 39.22660011456newton

Que según esta fórmula es la misma aplicada en sentido contrario del balón al pie.

La pelota al estar en reposo presenta una resistencia igual pero en sentido contrario en el momento del impacto, pero al ser obligada a moverse adquiere aceleración por la fuerza ejercida en ella.

Ahora calculamos su aceleración:

Recordemos que un Newton es la fuerza capaz de comunicarle la masa de un kilogramo la aceleración de 1 m/s2.

Entonces 39.22660011456n x 1m/s2 = 39.22660011456m/s2

La masa es la medida de la inercia que tienen los cuerpos, siendo la inercia la resistencia que presentan los cuerpos a cambiar su estado de reposo o de movimiento. Tenemos una masa de .450k

Usamos la formula F = ma, Pero como ya tengo la fuerza y la masa busco la fórmula para obtener la aceleración despejo pasando a m a dividir la fuerza y la nueva fórmula queda así a= F/m

F se mide en newton m - en kilogramos “a” en metros por segundo al cuadrado.

Ahora calculamos la aceleración con esta nueva fórmula: F/m = a

m =.450k

F= 39.22660011456newton

Sustituimos: a= F/m a = 39.22660011456/ .450 = 87.1702224768 m/s2.

La aceleración es de: 87.1702224768 m/s2.

Si el balón golpea un muro, con esa misma intensidad, será la reacción de impacto en sentido opuesto al que fue lanzado.

La acción de lanzarlo provoca el impacto con el muro

La reacción es el “rebote” con la misma intensidad pero en sentido contrario

Módulo 14 Semana 3 Prepa en Línea SEP Actividad "Eras geológicas"

Les comparto el texto de la actividad:

Era cenozoica (Era terciaria)

Es la última de las eras geológicas, literalmente significa de “la vida nueva”. Parte desde la extinción de los dinosaurios, y continúa hasta nuestros días. Es con toda propiedad la era del dominio de los mamíferos, destacando en ella notablemente el papel de nuestra especie.

A) CARACTERÍSTICAS FÍSICAS: Es una división de la escala temporal geológica, es la era geológica que se inició hace unos 66 millones de años y que se extiende hasta la actualidad. Se divide en tres periodos: Paleógeno, Neógeno y Cuaternario.

B) PRINCIPALES ESPECIES: Surgen distintos órdenes de mamíferos: marsupiales, ungulados, creodontos, lémures, mamuts, tigres dientes de sable, y el moderno homo sapiens en él cuaternario.

C) CLIMA/ TEMPERATURA

Paleógeno: Clima tropical y a finales del periodo Clima cálido.

Neógeno: Inicia con clima moderado, a finales presenta clima frío y seco.

Cuaternario: Da comienzo la reciente Edad de Hielo en el pleistoceno

y en el Holoceno finaliza la glaciación y surge la raza humana.

D) ACTIVIDAD VOLCÁNICA: Durante el Neógeno se presenta la orogenia en el hemisferio norte y la orogenia Alpina, los cinturones orogénicos están asociados a zonas de subducción, las cuales consumen corteza terrestre y producen volcanes, la subducción provoca muchos terremotos de gran magnitud. La subducción también causa la fusión parcial de parte del manto terrestre generando magma que asciende dando lugar a volcanes. En el Cenozoico se dio el volcanismo tipo intraplaca del Cenozoico. (Aranda.pdf)

E) LA SISMICIDAD Y TECTÓNICA DE PLACAS EN LA ERA CENOZOICA:

Geológicamente, el Cenozoico es la época en que los continentes se trasladaron a sus posiciones actuales. Australia-Nueva Guinea se separaron y derivaron al norte y se acercaron al Sureste de Asia. La Antártida se trasladó a su actual emplazamiento sobre el Polo Sur. El océano Atlántico se ensanchó, y más tarde, Sudamérica se unió a Norteamérica con la formación del istmo de Panamá.

En la actualidad, el proceso aún continúa en algunas zonas.

F) PRINCIPAL(ES) RASGO(S) QUE DISTINGUE(N) LA ERA CENOZOICA:

Rápida evolución y diversificación de la fauna, especialmente mamíferos. Importante evolución y dispersión de modernos tipos de plantas con flor. Orogenia Alpina. Formación de la corriente Circumpolar Antártica y congelación de la Antártida. Primeros mamíferos grandes (osos y pequeños hipopótamos). Aparecen las plantas modernas; los mamíferos se diversifican en varios linajes primitivos, tras el evento de extinción del Cretácico-Terciario, nace nueva vida en la era cenozoica.

G) CÓMO FAVORECIÓ LA ERA CENOZOICA LA EVOLUCIÓN DE LA VIDA.

Al Cenozoico también se le llama la era de los mamíferos, animales que, al extinguirse los dinosaurios a finales del Cretácico, sufrieron una extraordinaria radiación adaptativa y pasaron a ser la fauna característica. Hace unos 30 millones de años surgieron los primeros primates superiores (los más primitivos estaban ya presentes hace más 65 millones de años), aunque Homo sapiens no apareció hasta hace unos 200 000 años. Esta era favoreció la formación de la vida, ya que en ella la tierra alcanzo la temperatura ideal para el surgimiento y evolución de los primeros organismos, y se fue transformando la atmosfera, hasta ser apta para la evolución de los seres vivos.

sábado, 11 de noviembre de 2017

Módulo 14 Semana 3 "Calcular en moles" Prepa en Línea SEP

Calcular en moles

Química - Soluciones

IRMA ROBLES ALATORRE

20/07/2016

*******************************************************************************************************************************

El mol (molécula gramo)
Es una Unidad Internacional usada para medir la cantidad de una sustancia.
Un mol de una sustancia expresado en g es su masa molecular.
La Molaridad se representa con M mayúscula, para no confundir con Molalidad = (moles/Kg de solución) que se representa con m minúscula.

1. Resuelve los siguientes problemas, marca claramente el uso de fórmulas, procedimiento y resultado.

Problema 1.

Calcula ¿cuál es la concentración molar de una solución que se prepara disolviendo 58 gramos de NaCl en agua hasta formar un litro de disolución?
Nota: Redondea a números enteros las masas atómicas de los elementos.

A. Datos:

- NaCl = 58 g

- Volumen de la solución 1 L.

B. Fórmulas:

a) n = g de soluto / masa molecular

b) m = n / l de solución

La masa molecular es la suma de las masas atómicas de los elementos que forman el compuesto.

Utiliza la fórmula a para calcular el número de moles, sustituye los valores y efectúa las operaciones correspondientes.

Datos para solucionar el problema 1.

Solución: NaCl Elementos Na = Sodio Cl= Cloro V = 1Litro

Na Masa atómica 22.990 redondeamos a 23

Cl Masa atómica 35.453 redondeamos a 35

Sumamos la masa atómica de los elementos para obtener la masa molecular de NaCl

23+35= 58g por molécula

a) n = g de soluto / masa molecular

Sustituimos los valores de la fórmula n= 58g/58g./mol = 1mol

Con el número de moles calculado, utiliza la fórmula b, sustituyen los datos y efectúa las operaciones correspondientes.

b) molaridad = n/l de solución

Sustituyendo: m= 1 mol. /1 l de solución. = 1 mol/l

La concentración molar de esta solución es de 1 mol por litro

El número de partículas que existen en un mol (llamado número de Avogadro) de cualquier sustancia, se expresa en notación científica como: 6.023 x 1023 partículas. (Contenido extenso M14_S2 pag. 27)

Problema 2.

Calcula ¿cuál es la concentración molar de una solución que se prepara disolviendo 100 gramos de NaOH en agua hasta formar dos litros de disolución?

Nota: Redondea a números enteros las masas atómicas de los elementos.

A. Datos:

- NaOH = 100 g

- Volumen de la solución 2 l

B. Fórmulas:

a) n = g de soluto / masa molecular

b) m = n / l de solución

Recuerda: La masa molecular es la suma de las masas atómicas de los elementos que forman el compuesto.

Utiliza la fórmula a para calcular el número de moles, sustituye los valores y efectúa las operaciones correspondientes.

Compuesto: NaOH

Elementos: Na,=Sodio O= oxigeno H= Hidrogeno

Masa atómica de Na: 22.9898 Redondeamos a: 23

Masa atómica de O: 15.9994 Redondeamos a: 16

Masa atómica de H: 1.00794 Redondeamos a: 1

Masa molecular = 23+16+1= 40g. Por molécula.

a) n = g de soluto / masa molecular

n=100g./40g. n= 2.5g.
Con el número de moles calculado, utiliza la fórmula b, sustituyen los datos y efectúa las operaciones correspondientes.

b) molaridad = n/l de solución Volumen= 2L

molaridad=2.5/2 C. Resultado: molaridad =1.25mol

D. Explica brevemente tu respuesta, indicando por qué te dio ese resultado y qué significa.

El resultado es correcto porque obtuve los datos de la masa atómica de cada elemento que contienen las sustancias, consultándolos en la tabla periódica, luego seguí la indicación de redondear las cantidades para calcular con la suma de ellas el número de moles y luego con las formulas sustituí los valores para obtener la masa molecular y finalmente con la segunda fórmula para obtener la molaridad de la solución, que es el número de moles de soluto disuelto en cada litro de disolución.

“Para calcular el número de moles necesitas conocer el peso atómico (también llamado masa atómica) que se encuentra en la tabla periódica. Se expresa como g/mol. (gramos por mol). (Contenido extenso M14S2)

Y con la fórmula n= g de soluto/masa molecular obtenemos el número de moles.

Con el número de moles calculado, buscamos la molaridad con la segunda fórmula Molaridad = n/lts. de solución. Así encontramos la molaridad de cada sustancia que es el número de moles de soluto disuelto en cada litro de solución.

Fuentes:

Prepa en Línea SEP()Contenido extenso del módulo 14_S2_QA.pdf tema 13 “Disoluciones”

http://148.247.220.212/c4/mod/assign/view.php?id=4812